El cono es un cuerpo de revolución que representa en Diédrico con un triángulo en su proyección vertical y una circunferencia en su proyección horizontal.
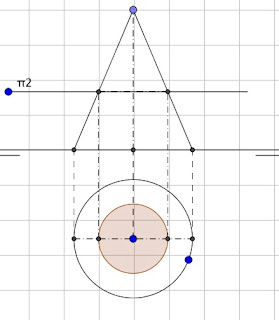
La primera sección y la más sencilla es con un plano horizontal, perpendicular al eje.
Como veis la sección es un círculo, si subimos el plano o lo bajamos el círculo aumenta o disminuye de diámetro. Diámetro que sale de la intersección del plano con las generatrices que forman el contorno de la proyección vertical.
En este caso el plano que corta es un plano proyectante vertical (plano de canto) que corta al eje. Esta sección se empieza resolviendo de la misma manera, la traza vertical del plano corta a las dos generatrices que forman la proyección vertical del cono, la bajamos y este segmento será el eje mayor de la elipse (la curva que produce esta sección).
Para hallar el eje menor, hacemos mediatriz del eje mayor que cortará a la traza con ese punto dibujamos la generatriz que llevamos hasta línea de tierra, después dibujamos las proyecciones horizontales de las generatrices, que se cortarán con la mediatriz en los extremos del eje menor de la elipse.
Podemos hacer cuantas generatrices queramos para sacar el mayor número de puntos de la ELIPSE. después podemos hacer la verdadera magnitud.
Os dejo los enlaces para que lo veáis mejor en le Geogebra y como siempre he dejado los puntos azules para que veáis otras posibilidades. Os recuerdo también, que tenéis que nombrar todos los puntos, las rectas y planos del dibujo.
Ánimo. Por lo visto ya no nos vemos hasta después de Semana Santa.




No hay comentarios:
Publicar un comentario